Computer Graphics - Transformation include the following topics: Linear Transformation, Homogeneous Coordinates, Affine Transformations, Inverse Transform, Composing Transform, 3D Transformations, Rodrigues' Rotation Formula.
CG-Modeling Transformation
Linear Transformation
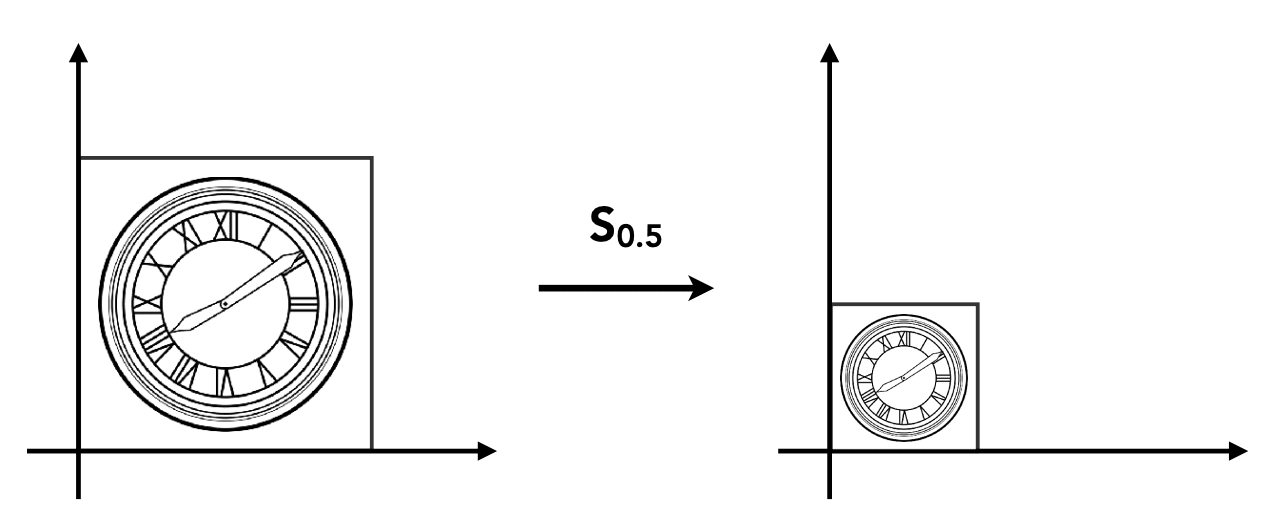
Scale Matrix
Reflection Matrix
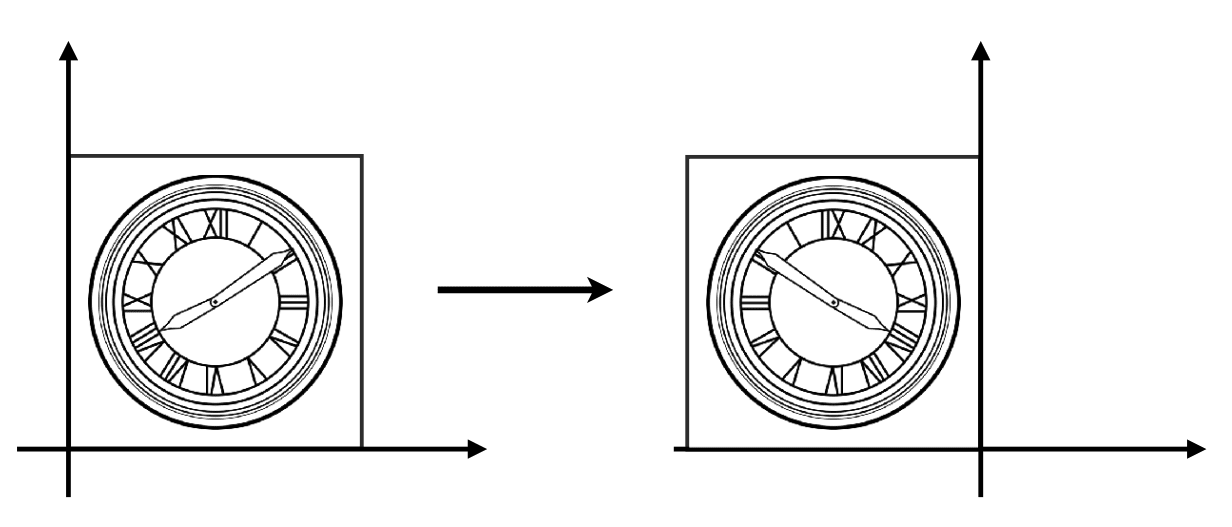
Horizontal reflection:
Shear Matrix
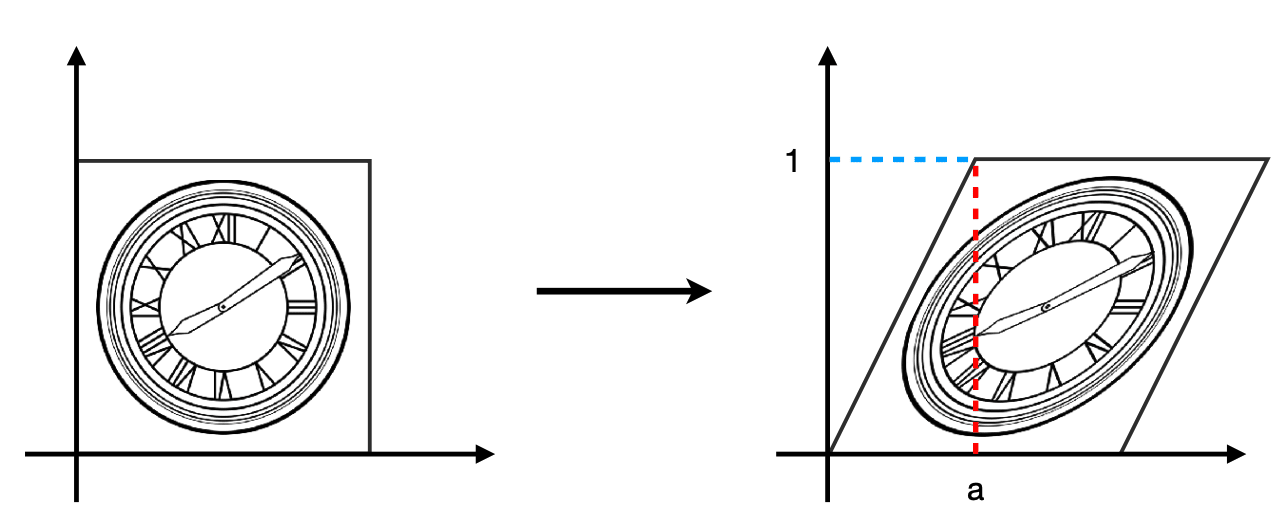
- Horizontal shift is
0at - Horizontal shift is
aat - Vertical shift is always
0
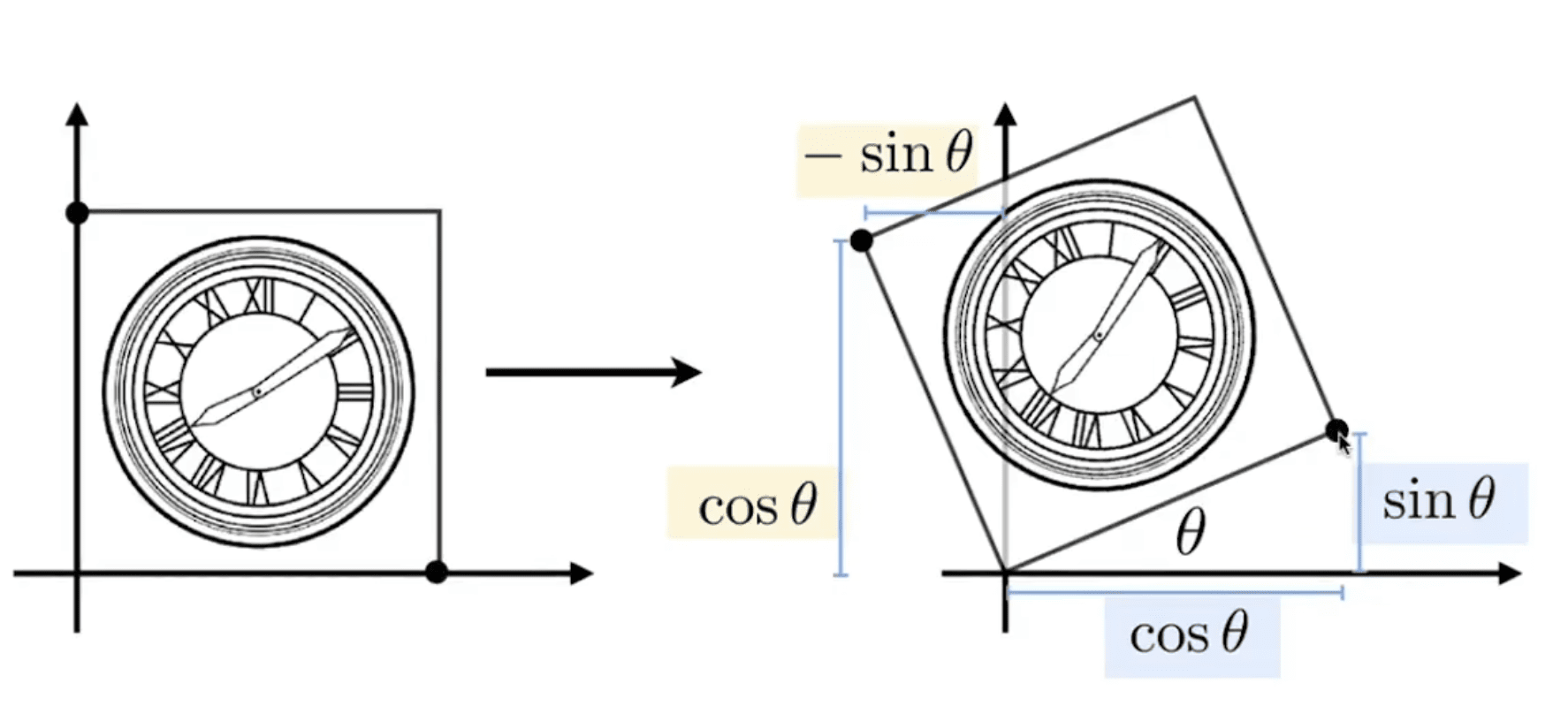
Rotation Matrix
Homogeneous Coordinates
Add a third coordinate (w-coordinate):
- 2D point:
- 2D vector:
Valid operations if w-coordinate of result is 1 or 0:
- vector
vector vector - point
point vector - point
vector point - point
point ??
Affine Transformations
Affine map = linear map + translation:
Using homogeneous coordinates:
Scale:
Rotation:
Translation:
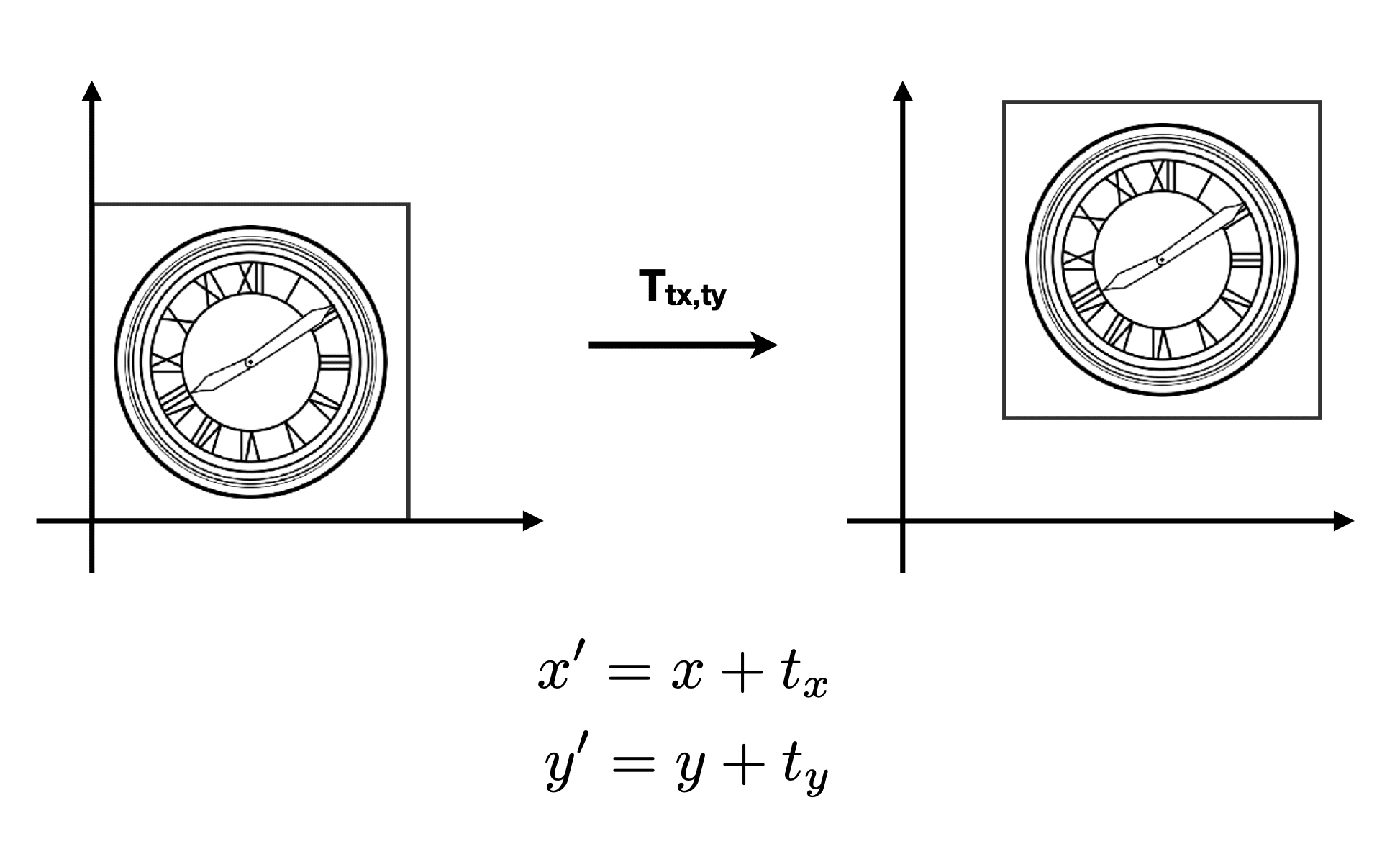
Inverse Transform
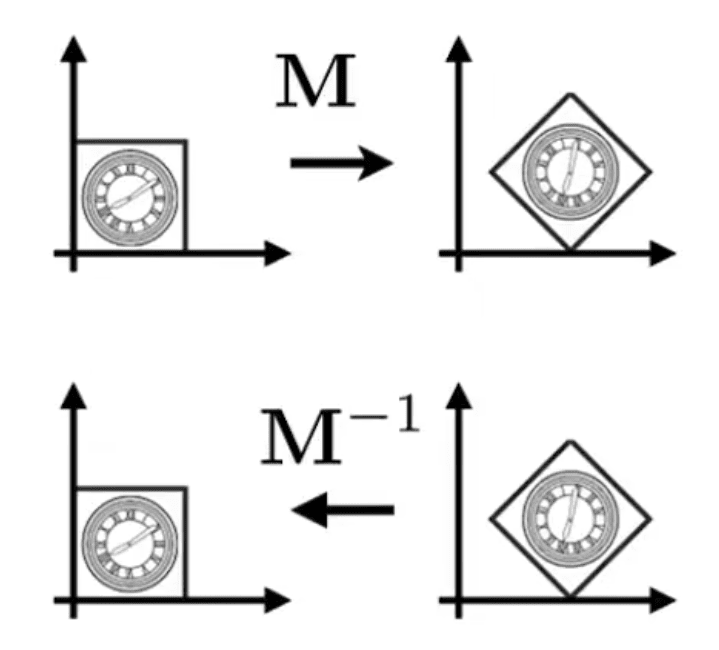
Composing Transform
Transform Ordering Matters!
Matrix multiplication is not commutative:
Note that matrices are applied right to left:
Sequence of Affine Transforms
- Compose by matrix multiplication
- Very important for performance!
Pre-multiply
How to rotate around a given point
- Translate center to origin
- Rotate
- Translate back
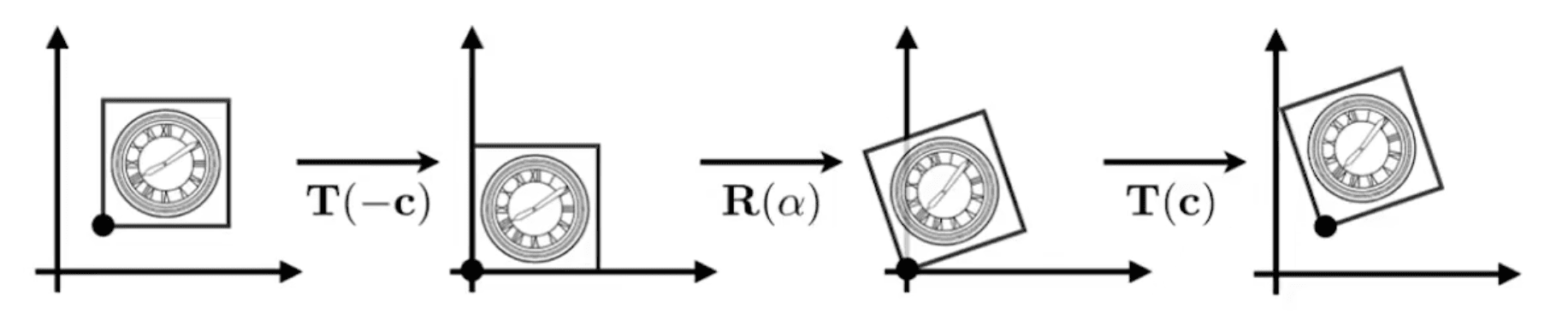
Matrix representation:
3D Transformations
Use homogeneous coordinates again:
3D point:
3D vector:
In general,
Use 4×4 Matrices for Affine Transformations
Order: Linear transformations, then translation.
Scale
Translation
Rotation
Rotation around the x-axis:
Rotation around the y-axis:
Rotation around the z-axis:
Compose Any 3D Rotation from
- So-called Euler angles
- Often used in flight simulators: roll, pitch, yaw

